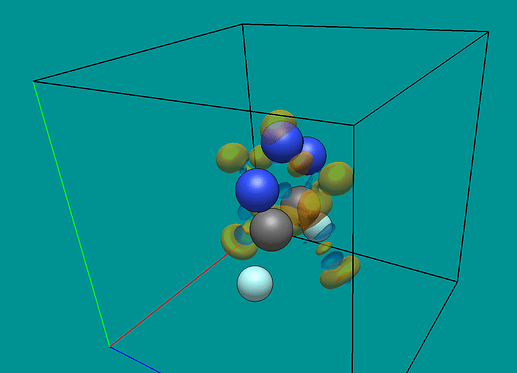
I’ve been using Quantum ESPRESSO quite a lot recently and have grown accustomed to printing out charge densities from it to XSF format. My primary use was reading in the charge densities and performing calculations with them, but I also would really like to be able to visualize those densities directly from the XSF file.
Currently as it stands I have to run another instance of pp.x from QE to print out a Gaussian Cube file, but these files are not quite the same since they do not include the unit cells from the calculation (and per my latest post, it is currently not possible to put one in after the fact). Realistically the format of a Gaussian Cube and an XSF from QE are almost identical, with the key difference being that the Gaussian Cube format doesn’t explicitly print a unit cell.
Reading in an XSF file is extremely similar to a Gaussian Cube, but there are two big differences, first being that while a Cube uses 6E13.5 for its output format, XSF files use 6E14.6 for the output format. From taking a look at the Avogadro source code though, I don’t actually think that the files are read in in byte strings and instead are just read in as lines and then split and converted.
The second difference is that an XSF file uses the full charge density and not the periodic charge density, which would need to be deleted to regain periodicity. Here’s a snippet of some Python code that I wrote that reads XSF files quite quickly (a fraction of a second slower than an equivalent in C++) and accounts for the periodicity:
def read_chg_dens_xsf(xsf_file: PathLike, crystal: Crystal):
with open(xsf_file, "rb") as xsf:
# Skip over atomic coordinate information
for _ in range(7 + crystal.get_num_atoms() + 3):
next(xsf)
# Pull size of FFT Grid
num_grid = [int(i) for i in next(xsf).strip().split()]
# Assign to variables to reduce indexing in loop
n_grid_0 = num_grid[0]
n_grid_1 = num_grid[1]
n_grid_2 = num_grid[2]
# Skip over misc. XSF data
for _ in range(4):
next(xsf)
# Calculate total number of datapoints in XSF file
n_points = n_grid_0 * n_grid_1 * n_grid_2
# Initialize indices
i = 0
j = 0
k = 0
# Allocate memory for charge density array
charge_density = np.zeros((n_grid_0, n_grid_1, n_grid_2))
# Loop over all data points in file
for index in range(n_points):
# Read in bytes for each data point, adding an extra if there is a newline character
charge_density[i][j][k] = xsf.read(14 + ((index + 1) % 6 == 0))
# Increment grid components to fill out array
i += 1
if i == n_grid_0:
i = 0
j += 1
if j == n_grid_1:
j = 0
k += 1
# Convert to periodic array
charge_density = np.delete(charge_density, [n_grid_0 - 1], axis=0)
charge_density = np.delete(charge_density, [n_grid_1 - 1], axis=1)
charge_density = np.delete(charge_density, [n_grid_2 - 1], axis=2)
return charge_density, num_grid
This code assumes that you’ve already parsed the header and stored the crystal vectors and the atomic coordinates.
The other differences of an XSF file are in the header, an example of which is included further down. There’s also two lines at the very end of the files from QE that say
END_DATAGRID_3D
END_BLOCK_DATAGRID_3D
Now, technically speaking you can determine the size of the unit cell from a Gaussian Cube within some precision limits by just taking the size of the grid (in the case of a Quantum ESPRESSO output this is the periodic FFT grid) and multiplying it by the vectors immediately after them, then converting units appropriately. For example, I have an XSF file from a calculation on a water molecule with a cubic unit cell of length 17.543876553 Angstrom. The header of the XSF file is
CRYSTAL
PRIMVEC
17.543876553 0.000000000 0.000000000
0.000000000 17.543876553 0.000000000
0.000000000 0.000000000 17.543876553
PRIMCOORD
3 1
O 8.770451552 9.174907782 8.771938274
H 9.544851428 8.573414302 8.771938274
H 8.000511848 8.567492748 8.771938274
BEGIN_BLOCK_DATAGRID_3D
3D_PWSCF
BEGIN_DATAGRID_3D_UNKNOWN
217 217 217
0.000000 0.000000 0.000000
17.543877 0.000000 0.000000
0.000000 17.543877 0.000000
0.000000 0.000000 17.543877
and the header of a Gaussian Cube file created from the exact same QE calculation is
Cubefile created from PWScf calculation
Contains the selected quantity on a FFT grid
3 0.000000 0.000000 0.000000
216 0.153487 0.000000 0.000000
216 0.000000 0.153487 0.000000
216 0.000000 0.000000 0.153487
8 0.000000 16.573751 17.338063 16.576561
1 1.000000 18.037155 16.201405 16.576561
1 1.000000 15.118776 16.190215 16.576561
which when we take 216 * 0.153487 * 0.529177249 we get 17.5439149, which is pretty close to the actual cell size of 17.543876553 Angstrom.